The Science of Orlando Jax
Gravity II - Orbits
The Claw is an atmosphere capable ship. Jax and his pirate crew take the ship to the surface of planets on a regular basis, both for a bit of plunder and R&R. But we know that interacting with planets can be a tricky and dangerous activity all because of that mysterious force gravity. So just what is the deal if you want to take a space ship anywhere near a big thing like a planet?
For the moment let's put aside the idea that we have a gravity plate, or a space-time field grabber, and assume that we have to do this the old fashioned way. Our ship (and us) will experience the gravitational force in accordance with the formula that we've seen before:

As the distance (r) between our ship and the planet gets smaller, the gravitational force we experience gets stronger quickly (that is r2 working). The ship has a velocity. If we assume that velocity is tangential to the gravitational force we can draw a representation of our situation as follows:
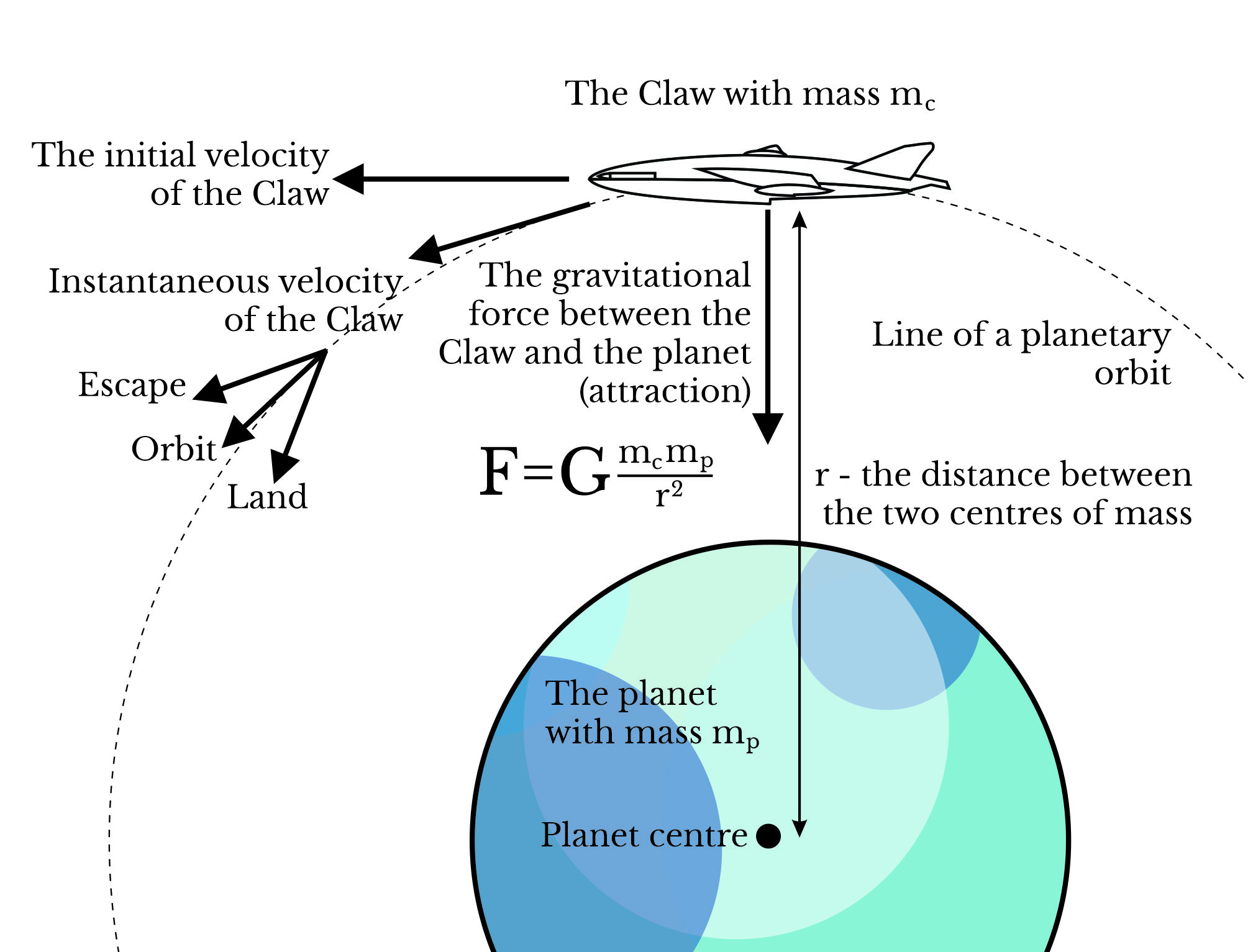
The gravitational force between The Claw and the planet is given by the F=G equation. Force can also be thought of in terms of mass and acceleration using the very well know equation F=ma. So the gravitational force, at any given point in time is trying to accelerate The Claw and the planet together. This acceleration translates into a velocity component. So the actual velocity of The Claw is a vector created by its own velocity and that created by the gravitational force - in the figure above I describe this as the instantaneous velocity. This instantaneous velocity wants to pull the Claw away from its original path and down towards the planet. In effect The Claw begins to fall around the planet.
With this falling idea, and assuming for the time being we don't fiddle with our speed, there are three possible outcomes. If The Claw's initial velocity is not great enough, the gravitational force will pull it down and if Jax isn't paying attention The Claw will crash on the surface of the planet.
If The Claw's initial velocity is big enough, the gravitational force will still pull The Claw towards the planet altering its course but The Claw's speed means it can escape the gravitational force and zoom off.
Finally if the velocities and forces line up, The Claw can enter a stable orbit around the planet. The Claw falls around the planet but has the correct velocity to neither escape nor crash.
So the upshot is that if we don't have a gravity plate, or a space-time field grabber, Jax can control the orbit of The Claw using its velocity relative to the planet. There is a way of calculating the velocity necessary to stay in an orbit. We can do this by combining the gravitational force equation with an equation for centripetal force. Thanks to Swinburne University for this definition:
The force needed by a body of mass m, to keep in a circular motion at a distance r, from the centre of a circle with velocity v, is the centripetal force F giving us:
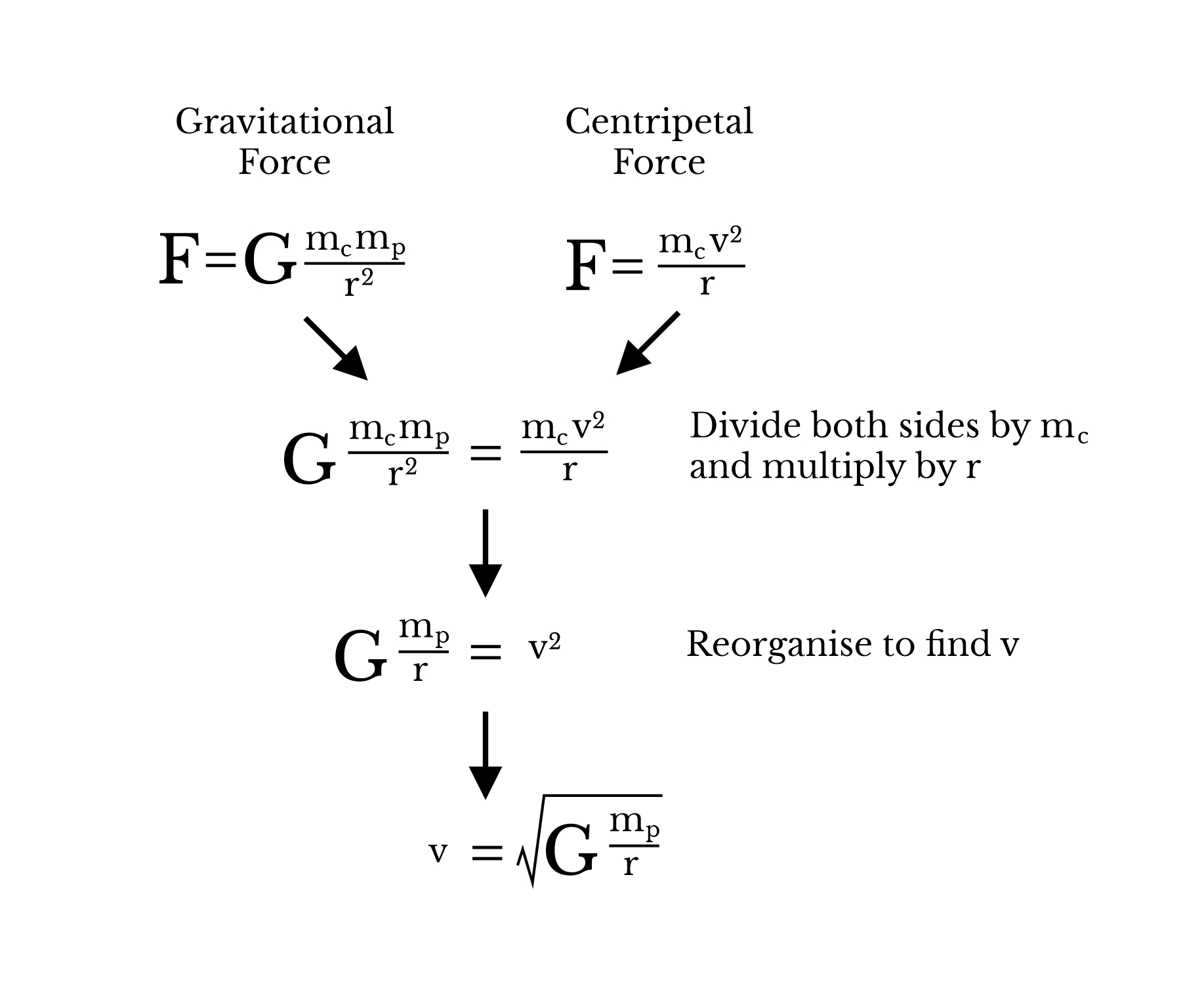
So given that we know the mass and radius, and the value of G, we can work out these orbit velocities for the Earth at least:
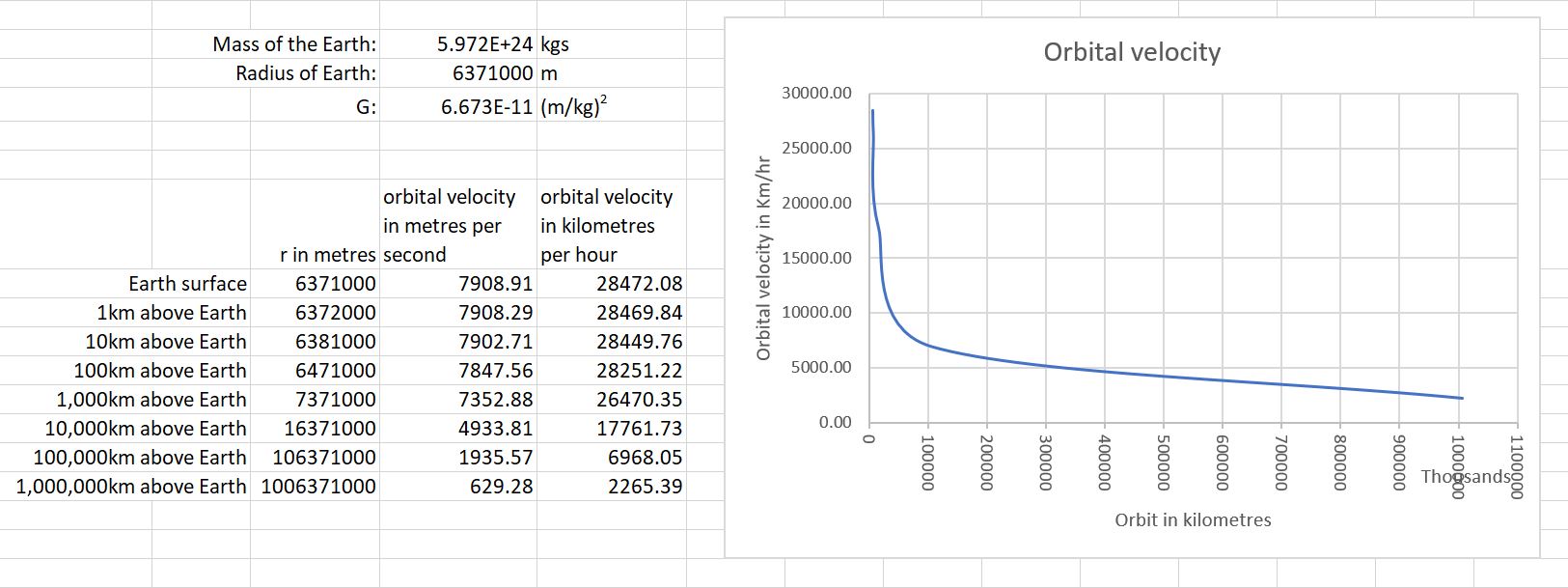
According to that, it's only after 10,000km that the velocity needed to stay in orbit begins to decrease significantly. But I think that shows that Jax, by controlling the velocity of The Claw, would be able to raise and lower his orbit - to land on a planet or escape it. The Claw would need an interesting sensor and instrument, one that can detect and measure gravity, and estimate the size of and distance to a planet and thus determine its mass. That data can then be used to calculate the thrust needed for in-orbital manoeuvres.
But hang on ...
Everything I've written is dealing in approximation. The equations are Newtonian - beautifully simple to understand and use but, thanks to Einstein, we now know not to be the whole story. For me, most profound and mind-boggling is the idea that as The Claw draws near to a planet it continues on a straight line through space time. The vast mass of the planet and its gravity actually bends space time so to the casual observer The Claw would appear to be going round in circles. How do we represent that idea? Amazing.
Other things:
- The equations do not take into account atmospheric drag. Hit the atmosphere and you start slowing down (and heating up) very rapidly,
- Bodies in space actually orbit a mid point based on their collective mass. The Earth is so big compared to the moon that we think of the Moon going round the Earth. In fact the Earth is orbiting this "mid point" - it just happens to be within the radius of the Earth,
- Real orbits are very rarely perfect circles but rather elipses - something Kepler worked out back in 1619.
Those animations
My animations are just that - simple things to demonstrate an idea. I could have been more rigorous and tried to develop simulations based on the actual equations discussed in this post. Then there is the opportunity to go even further and create simulations based on Einstein rather than Newton but I think that is for another day. If you are interested in seeing how those animations work, have a look at the code on github.